 |
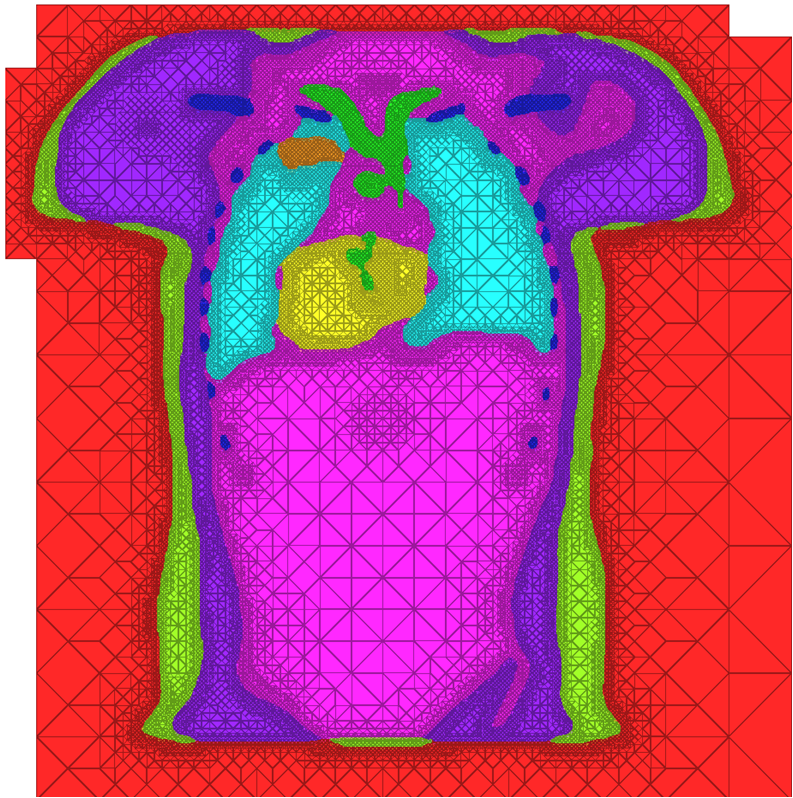
| A cross-section of a 3-dimensional, tetrahedral mesh of a torso. Each separate organ type is shown using a different color. |
High Quality Meshing
The problem of mesh generation has been widely studied, as a hybrid field of interest to the scientific, engineering, and computer science communities. In each of these fields, meshes are used to compute numerical approximations to solutions of partial differential equations. To do so, continuous mathematics are replaced with a discrete analogue, most commonly to facilitate the finite element method (FEM).The FEM works by decomposing a domain of interest into discrete entities of various dimensions, such as points (0-dimensional), edges (1-dimensional), and cells of higher dimension (frequently triangles and quadrilaterals are used for 2-dimensionl elements, tetrahedra and hexahedra for 3-dimensional). Together, these elements form what is commonly called a mesh (see figure)Solutions to the complex system are solved piecewise on each element, and then aggregated together to form the final solution. The FEM has become an important tool in medical imaging as well. For example, CT scans of legs can be meshed so that orthopedic modeling can accurately simulate gait, MRI scans of the torso are frequently used in cardiac electrophysical modeling, and images of the skull can identify structures of the brain.
Because the FEM is a computational tool that processes individual elements to approximate a whole solution, it is deeply impacted by the mesh elements used to represent the space. Two principle concerns stand out in the meshing problem for medical images:
- The representation quality of surfaces within the domain, or how well the mesh conforms to a boundary. For example, when meshing anatomical structures such as the lungs, heart, bones, and liver in a torso, capturing these surfaces can be of critical importance for proper modeling of simulation behavior. Similarly, work over the past year has shown that to simulate electrical behavior of implanted cardiac defibrilators requires careful modeling of the device itself.
- The shapes of mesh elements, in particular the spacing, orientation, and angles that adjacent elements form. Shape plays a significant role in the computations performed on meshes. For example, the dihedral angles that each tetrahedra has affects the numeric conditioning of matrices used in the FEM solve. As these angles near either 0 or 180 degrees, solutions degenerate because of a lack of computational precision, and often require additional computational effort. Meshing that satisfy both of these quality concerns is a major challenge, since often improving one of them comes at the expense of degenerating the other.
Current Research Progress
Our image-to-simulation pipeline has been built using BioMesh3D for our meshing needs. BioMesh3D's major strength is its ability to build extremely high quality (in terms of surface representations and element shape) tetrahedral mesh representations of medical image data. However, constructing these high quality meshes comes with a large computational cost, primarily at the optimization-driven particle distribution stage. Our work in the past year has been developing a complementary meshing algorithm to address these concerns.Our newest meshing algorithm, MMStuff, uses a stencil-based approach based on a popular isosurface stuffing algorithm (see F. Labelle and J. R. Shewchuk, ACM Trans. Graph., 2007). This algorithm has two principle advantages for meshing: (1) it is computationally very efficient because it minimizes necessary work by applying a stencil repeatedly and (2) it produces excellent tetrahedral elements, that are important for simulation quality on which these meshes will be used. The stenciling technique of isosurface stuffing can produce meshes which are boundary-conforming to single surfaces. However, when the data is segmented, the surfaces of interest form a complex, non-manifold configuration, which requires a completely redesigned meshing scheme.
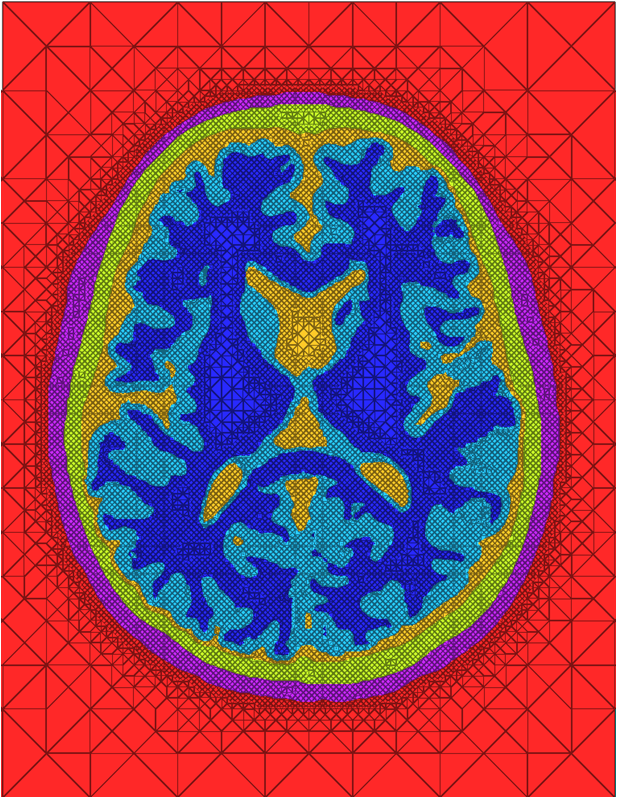
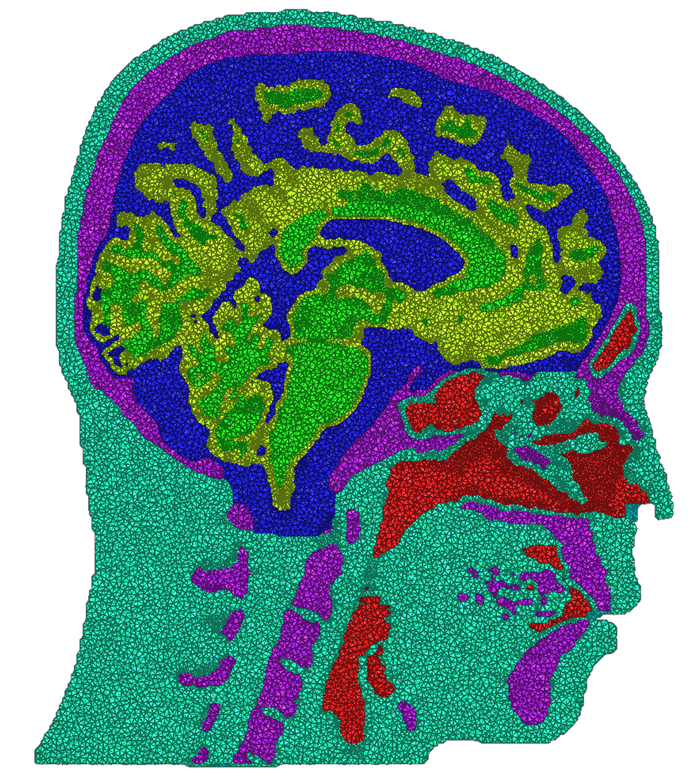
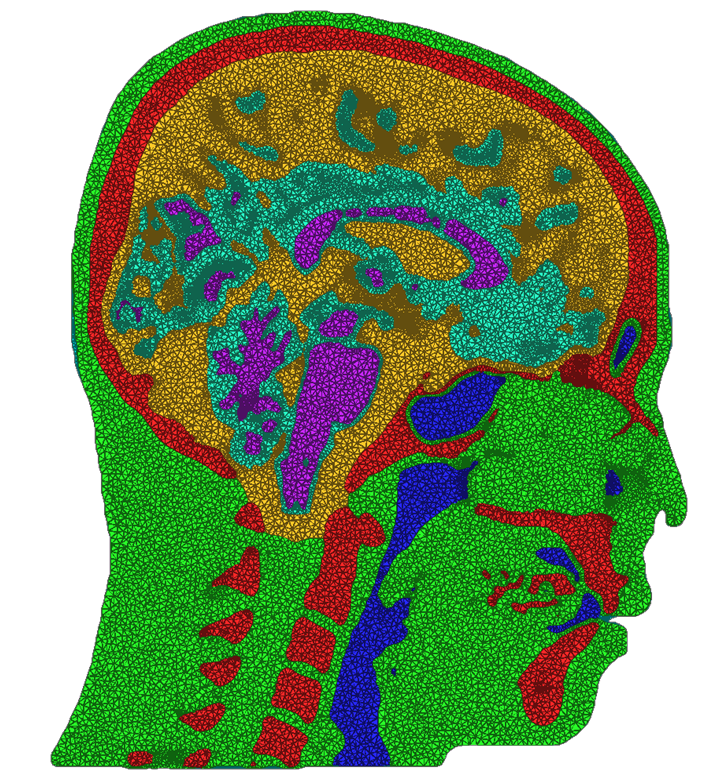
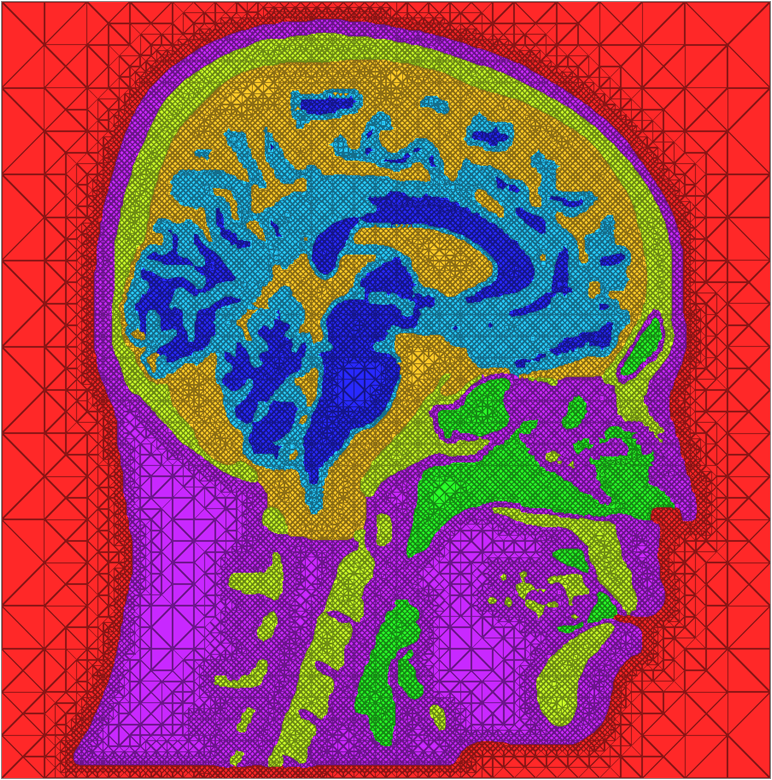
We have developed and implemented a stuffing-like algorithm for multimaterial surfaces. This algorithm produces excellent tetrahedral meshes that conform to complex, non-manifold surfaces commonly found in segmented medical images. These meshes are graded in resolution - they use the smallest scale elements near to the surface, but are frugal and use larger mesh elements at greater distances. Figure above shows two meshes produced by MMStuff, one of a human skull with labeled segmentations of the brain and the second of a CT scan of an orange with label elements of the fruit anatomy. The major research contribution is the first stuffing-like algorithm for segmented datasets that guarantees on the dihedral angles for each tetrahedra in the mesh. In fact, we have shown that MMStuff is not only faster than BioMesh3D, but its scheme also for flexibility in either building high quality tetrahedral elements or building geometrically smooth representations of the boundary surfaces.
A second component of this work was studying the impacts of different meshing techniques on biomedical simulations. We compared the meshes created by MMStuff with those created by both BioMesh3D and the meshing algorithm for image data available in the popular Computational Geometry Algorithms Library, or CGAL (http://www.cgal.org). This continues a set of ongoing work to study the importance of capturing boundary surfaces and using high quality mesh elements. Our results were inspiring---in addition to constructing meshes of millions of elements in only a few seconds, MMStuff also produced comparable or higher quality meshes than the more expensive BioMesh3D and CGAL algorithms. Figure below highlights a comparison between meshes produced by all three software packages.
 |
 |
 |
| Cross sections of meshes generated by BioMesh3D (left), CGAL (middle), and MMStuff (right) | ||
MeshMed Workshop
CIBC members are co-organizing the second appearance of a series of workshops on Mesh Processing in Medical Image Analysis, held in conjuncture with MICCAI 2012 at Nice, France. This workshop continues the goal of gathering those who create the data, those who write geometric software, and those who use meshes for simulation. This workshop proposes to improve the cross-pollination of the imaging and meshing efforts by considering how meshing fits into the end-to-end pipeline from image acquisition to clinical analysis. A major goal is identifying the meshing needs of the medical community, which frequently uses the image-to-simulation pipeline, but is required to piece together individual pieces. CIBC's focus is a centralized effort, where end users can elect to use individual components of the pipeline as well as take advantage of the interconnections within the whole.References
1. BioMesh3D: Quality Mesh Generator for Biomedical Applications. Scientific Computing and Imaging Institute (SCI)2. J. R. Bronson, D. Swenson, J. A. Levine, and R. T. Whitaker. Conforming, tetrahedral meshing of image data for biomedical simulation. Technical report, 2012.
3. D. J. Swenson, J. A. Levine, Z. Fu, J. Tate, and R. S. MacLeod. The effect of non-conformal finite element boundaries on electrical monodomain and bidomain simulations. Computing in Cardiology, 37:97 {101,Sept. 2010.}